Pourquoi les écoles américaines et britanniques enseignent-elles différentes méthodes de calcul de l'écart-type?

15

Si je comprends bien, les écoles britanniques enseignent que l'écart-type se trouve en utilisant:

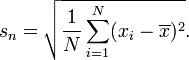
$texte alternatif$

alors que les écoles américaines enseignent:

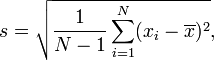
$texte alternatif$

(au niveau de base de toute façon).

Cela a causé un certain nombre de problèmes à mes étudiants dans le passé, car ils ont cherché sur Internet, mais ils ont trouvé la mauvaise explication.

Pourquoi la différence?

Avec des ensembles de données simples, par exemple 10 valeurs, quel degré d'erreur y aura-t-il si la mauvaise méthode est appliquée (par exemple dans un examen)?

standard-deviation error teaching unbiased-estimator Amos
la source

4

Je ne sais pas si caractériser l'une ou l'autre comme la «mauvaise» formule est la façon de comprendre le problème. C'est juste que le second est «meilleur» dans le sens où il s'agit d'un estimateur non biaisé de l'écart-type réel. Donc, si vous vous souciez d'estimations impartiales, la seconde est «meilleure» / «correcte».

Je caractérisais la formule comme "fausse" uniquement en ce sens que dans un examen, si vous utilisez la formule qui n'est pas proscrite par le programme, vous vous retrouverez avec la "mauvaise" réponse. De plus, si les valeurs ne sont pas un échantillon de population en soi, la première formule donne sûrement la valeur la plus précise.

Amos

14

Srikant, je ne pense pas que le second soit un estimateur non biaisé. Le carré de celui - ci est un estimateur non biaisé de la vraie variance. Cependant, l'inégalité de Jensen établit que l'espérance d'une fonction curviligne d'une variable aléatoire n'est pas la même que la fonction de l'espérance de la variable aléatoire. Par conséquent, la deuxième formule ne peut pas être un estimateur non biaisé de la véritable déviation standard.

Andrew Robinson

Pour référence croisée: il a également été demandé @ m.SE ...

JM n'est pas statisticien

4

Toute école américaine utilisant le texte élémentaire très populaire de Freedman, Pisani et Purves utilise la première formule (

), il semble donc incorrect de caractériser cela comme une différence entre les États-Unis et le Royaume-Uni.

s_{n}

$s_n$

whuber

18

La première formule est l' écart type de la population et la deuxième formule est l' écart type de l' échantillon . La deuxième formule est également liée à l'estimateur non biaisé de la variance - voir wikipedia pour plus de détails.

Je suppose (ici) au Royaume-Uni qu'ils ne font pas la distinction entre l'échantillon et la population au lycée. Ils ne touchent certainement pas à des concepts tels que les estimateurs biaisés.

csgillespie
la source

4

Colin, un estimateur non biaisé de l'écart-type n'a pas de représentation sous forme fermée dans le cas général. Ce qui existe, c'est l'estimateur non biaisé de la variance (s 2 dans ce cas). Il convient de noter que les deux sont des estimateurs cohérents de la variance de la population - et donc par le théorème de la cartographie continue, sont les deux estimateurs des écarts-types. Un point connexe est que s n 2 a un MSE inférieur à s 2 . L'avantage supplémentaire d'imposer l'impartialité est discutable.

mornington

@Tirthankar - très bâclé de ma part. J'ai légèrement modifié la réponse. Merci.

csgillespie

2

Pour autant que je m'en souvienne, on m'a enseigné le calcul de `` l'échantillon '' en mathématiques et en sciences GCSE (14-16 ans) et la distinction entre les populations et les échantillons et leurs mesures de variance associées a été couverte (mais pas en profondeur) au niveau A ( 16-18 ans). Je ne suis donc pas sûr que ce soit une simple différence entre le Royaume-Uni et les États-Unis.

Freya Harrison du

11

Parce que personne n'a encore répondu à la dernière question - à savoir, pour quantifier les différences entre les deux formules - prenons soin de cela.

Pour de nombreuses raisons, il convient de comparer les écarts-types en termes de ratios plutôt que de différences. Le rapport est

s_{n} / s = \sqrt{\frac{N - 1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2 N} .

$s_n / s = \sqrt{\frac{N-1}{N}} = \sqrt{1 - \frac{1}{N}} \approx 1 - \frac{1}{2N}.$

L'approximation peut être considérée comme tronquant la série de Taylor (alternée) pour la racine carrée, indiquant que l'erreur ne peut pas dépasser $|\binom{1/2}{2}N^{-2}|$ $1 / (8 N^2)$ $N$ $2$

$N$ $5$ $N$ $10$ SD, comme lors de la comparaison des écarts de deux ensembles de données. (Lorsque les ensembles de données sont équitables, les écarts disparaissent effectivement et les deux formules conduisent à des conclusions identiques.) Il s'agit sans doute des formes de raisonnement que nous essayons d'enseigner aux élèves débutants, donc si les élèves se demandent quelle formule utiliser, cela pourrait être considéré comme un signe que le texte ou la classe ne met pas l'accent sur ce qui est vraiment important.

$N$ $t$ $z$ $s$ $s_n$

whuber
la source

6

Ceci est la correction de Bessel . La version américaine montre la formule de l' écart-type de l' échantillon , où la version britannique ci-dessus est l' écart-type de l'échantillon .

Reed Copsey
la source

5

Je ne suis pas sûr que ce soit un problème purement américain contre britannique. Le reste de cette page est extrait d'une FAQ que j'ai écrite ( http://www.graphpad.com/faq/viewfaq.cfm?faq=1383 ).

Comment calculer la SD avec n-1 dans le dénominateur

Calculez le carré de la différence entre chaque valeur et la moyenne de l'échantillon.
Ajoutez ces valeurs.
Divisez la somme par n-1. Le résultat est appelé la variance.
Prenez la racine carrée pour obtenir l'écart-type.

Pourquoi n-1?

Pourquoi diviser par n-1 plutôt que n lors du calcul d'un écart-type? À l'étape 1, vous calculez la différence entre chaque valeur et la moyenne de ces valeurs. Vous ne connaissez pas la véritable moyenne de la population; tout ce que vous savez, c'est la moyenne de votre échantillon. À l'exception des rares cas où la moyenne de l'échantillon est égale à la moyenne de la population, les données seront plus proches de la moyenne de l'échantillon que de la vraie moyenne de la population. Ainsi, la valeur que vous calculez à l'étape 2 sera probablement un peu plus petite (et ne peut pas être plus grande) que ce qu'elle serait si vous utilisiez la moyenne réelle de la population à l'étape 1. Pour compenser cela, divisez par n-1 plutôt que nv C'est ce qu'on appelle la correction de Bessel.

Mais pourquoi n-1? Si vous connaissiez la moyenne de l'échantillon et toutes les valeurs sauf une, vous pourriez calculer quelle doit être cette dernière valeur. Les statisticiens disent qu'il y a n-1 degrés de liberté.

Quand la SD doit-elle être calculée avec un dénominateur de n au lieu de n-1?

Les livres de statistiques montrent souvent deux équations pour calculer la SD, l'une en utilisant n et l'autre en utilisant n-1, dans le dénominateur. Certaines calculatrices ont deux boutons.

L'équation n-1 est utilisée dans la situation courante où vous analysez un échantillon de données et souhaitez tirer des conclusions plus générales. Le SD calculé de cette façon (avec n-1 dans le dénominateur) est votre meilleure estimation de la valeur du SD dans la population globale.

Si vous souhaitez simplement quantifier la variation dans un ensemble particulier de données et ne prévoyez pas d'extrapoler pour tirer des conclusions plus larges, vous pouvez calculer la SD en utilisant n dans le dénominateur. Le SD résultant est le SD de ces valeurs particulières. Cela n'a aucun sens de calculer la SD de cette façon si vous voulez estimer la SD de la population à partir de laquelle ces points ont été tirés. Cela n'a de sens d'utiliser n dans le dénominateur que lorsqu'il n'y a pas d'échantillonnage d'une population, il n'y a pas de désir de tirer des conclusions générales.

Le but de la science est presque toujours de généraliser, donc l'équation avec n au dénominateur ne doit pas être utilisée. Le seul exemple auquel je peux penser où cela pourrait avoir un sens est de quantifier la variation entre les résultats des examens. Mais beaucoup mieux serait de montrer un nuage de points de chaque score, ou un histogramme de distribution de fréquence.

Harvey Motulsky
la source

1

Je ne suggérais pas que c'était le cas, j'étais simplement curieux de savoir pourquoi une telle différence avait pu survenir, quel genre de niveau d'erreur suite au mauvais conseil pourrait donner et s'il y avait une explication décente de la différence que je pouvais donner à mes étudiants .

Amos

@harvey - le lien est mort

baxx

1

@baxx .. Merci de l'avoir signalé. Fixé.

Harvey Motulsky

3

Puisque N est le nombre de points dans l'ensemble de données, on pourrait faire valoir qu'en calculant la moyenne, on a réduit le degré de liberté dans l'ensemble de données de un (car on a introduit une dépendance dans l'ensemble de données), donc on devrait utiliser N -1 lors de l'estimation de l'écart-type d'un ensemble de données dont il fallait auparavant estimer la moyenne.

Benjamin Bannier
la source

Pourquoi les écoles américaines et britanniques enseignent-elles différentes méthodes de calcul de l'écart-type?

Réponses: