Évaluation des modèles de régression logistique

Cette question découle de ma confusion réelle sur la façon de décider si un modèle logistique est assez bon. J'ai des modèles qui utilisent l'état des couples projet individuel deux ans après leur formation en tant que variable dépendante. Le résultat est réussi (1) ou non (0). J'ai des variables indépendantes mesurées au moment de la formation des paires. Mon objectif est de tester si une variable qui, selon moi, influencerait le succès des paires a un effet sur ce succès, en contrôlant d'autres influences potentielles. Dans les modèles, la variable d'intérêt est significative.

Les modèles ont été estimés à l'aide de la glm()fonction dans R. Pour évaluer la qualité des modèles, j'ai fait quelques choses: glm()vous donne le residual deviance, le AICet le BICpar défaut. De plus, j'ai calculé le taux d'erreur du modèle et tracé les résidus groupés.

Le modèle complet a une déviance résiduelle plus petite, AIC et BIC que les autres modèles que j'ai estimés (et qui sont imbriqués dans le modèle complet), ce qui m'amène à penser que ce modèle est "meilleur" que les autres.
Le taux d'erreur du modèle est assez faible , à mon humble avis (comme dans Gelman et Hill, 2007, pp.99 ) :,
error.rate <- mean((predicted>0.5 & y==0) | (predicted<0.5 & y==1) aux alentours de 20%.

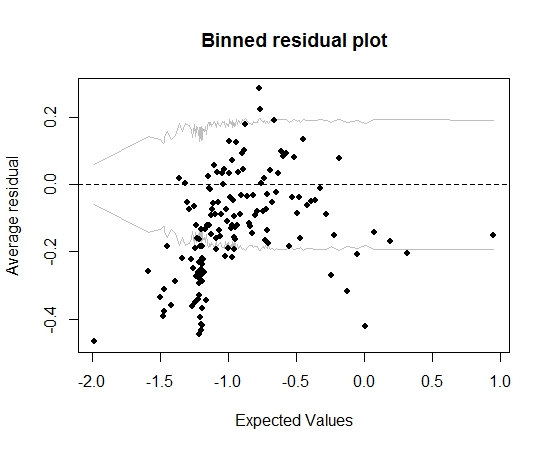
Jusqu'ici tout va bien. Mais lorsque je trace le résidu de la poubelle (toujours à la suite des conseils de Gelman et Hill), une grande partie des bacs se situent en dehors de l'IC à 95%: Parcelle des résidus en attente

Cette intrigue m'amène à penser qu'il y a quelque chose de complètement faux dans le modèle. Cela devrait-il m'amener à jeter le modèle? Dois-je reconnaître que le modèle est imparfait mais le conserver et interpréter l'effet de la variable d'intérêt? J'ai joué avec l'exclusion des variables à leur tour, et aussi une certaine transformation, sans vraiment améliorer le tracé des résidus groupés.

Éditer:

À l'heure actuelle, le modèle comporte une douzaine de prédicteurs et 5 effets d'interaction.
Les couples sont "relativement" indépendants les uns des autres dans le sens où ils se forment tous sur une courte période (mais pas à proprement parler, tous simultanément) et qu'il y a beaucoup de projets (13k) et beaucoup d'individus (19k ), donc une bonne partie des projets ne sont rejoints que par une seule personne (il y a environ 20000 paires).

r logistic goodness-of-fit residuals Antoine Vernet
la source

Une estimation approximative de la taille minimale de l'échantillon nécessaire pour faire ce que vous faites est que vous avez besoin que le minimum du nombre d'événements ou le nombre de non-événements dépasse 15 fois (12 + 5), en supposant que vous avez eu 17 termes candidats en le modèle. Si vous avez fait un dépistage des prédicteurs, en utilisant

Y

$Y$

D'après ce que vous dites, la taille de l'échantillon ne semble pas être un problème, car j'ai environ 20000 milliers de paires (dont environ 20% réussissent).

Antoine Vernet

Réponses:

La précision de la classification (taux d'erreur) est une règle de notation incorrecte (optimisée par un modèle bidon), arbitraire, discontinue et facile à manipuler. Ce n'est pas nécessaire dans ce contexte.

Vous n'avez pas indiqué le nombre de prédicteurs. Au lieu d'évaluer l'adéquation du modèle, je serais tenté de simplement adapter le modèle. Une approche de compromis consiste à supposer que les interactions ne sont pas importantes et à permettre aux prédicteurs continus d'être non linéaires à l'aide de splines de régression. Tracez les relations estimées. lerms package en R rend tout cela relativement facile. Voir http://biostat.mc.vanderbilt.edu/rms pour plus d'informations.

Vous pourriez élaborer sur les «paires» et si vos observations sont indépendantes.

Frank Harrell
la source

Si je comprends bien, votre conseil est de vous concentrer sur l'intrigue des résidus et de rectifier celui-ci avant de faire quoi que ce soit d'autre, éventuellement en utilisant des splines de régression, ai-je raison? J'ai édité la question pour indiquer combien il existe de prédicteurs et que les paires sont "relativement" indépendantes.

Antoine Vernet

Salut @Frank. Pourquoi dites-vous que la précision de la classification est une mauvaise méthode? Est-ce parce qu'il est ici évalué sur les mêmes données où le modèle est dérivé?

Peter Flom - Réintégrer Monica

Non, mon commentaire n'était pas de se concentrer sur les parcelles résiduelles, mais plutôt de faire en sorte que le modèle soit "à l'avant". Peter, la proportion classée «correctement» présente de multiples problèmes, notamment le fait qu'il s'agit de l'estimateur de précision la plus faible des performances prédictives, est arbitraire et conduira à la sélection du mauvais modèle. J'ai un exemple où l'ajout d'un prédicteur très fort (sur la base du rapport de vraisemblance

χ^{2}

$\chi^2$ ou

c

$c$ -index (zone ROC) fait diminuer de manière significative la proportion correctement classée .

Frank Harrell

Non, je veux dire permettre aux prédicteurs continus de fonctionner de façon non linéaire sur l'échelle des cotes logarithmiques, en les développant en plusieurs termes en utilisant des splines cubiques restreintes (splines naturelles). Tracez ensuite les transformations estimées pour en savoir plus sur les effets partiels de chaque prédicteur.

Frank Harrell

Merci pour la contribution, c'était vraiment utile. En approfondissant les données, j'ai réalisé que j'avais des problèmes de colinéarité (même si je n'avais pas de corrélations par paires élevées).

Antoine Vernet

La situation semble un peu étrange, mais je pense que votre intrigue peut fournir un indice. Il semble qu'il puisse y avoir une relation curviligne. Il est permis d'utiliser des termes polynomiaux et d'autres transformations de variables prédictives (par exemple, $x^2$ ) en régression logistique, tout comme en régression OLS. Cela pourrait valoir la peine d'essayer.

gung - Réintégrer Monica
la source