Comment penser la porte Z dans une sphère Bloch?

10

Je ne sais pas comment comprendre la porte $Z$ dans une sphère Bloch.

Compte tenu de la matrice $Z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$ il est compréhensible que $Z|0\rangle = |0\rangle$ et $Z|1\rangle = -|1\rangle$ .

Il est expliqué ici que la porte $Z$ est une rotation $\pi$ autour de l' axe $Z$ Alors, comment dois-je comprendre $Z|1\rangle = -|1\rangle$ ? Depuis $|1\rangle$ est le pôle sud, je pense qu'il est naturel de penser que $\pi$ rotation autour du $Z$ axe ne fait rien.

quantum-gate bloch-sphere Bick
la source

7

La façon de penser à la sphère de Bloch est en termes de matrice de densité pour l'état. agissant soit sur ou ne fait rien, comme c'est le cas pour toute matrice de densité diagonale. Pour voir l'effet de la rotation, vous devez regarder comment toute matrice de densité non diagonale est modifiée par , comme . $Z$ $|0\rangle\langle 0|$ $|1\rangle\langle 1|$ $Z$ $|+\rangle\langle +|$

DaftWullie
la source

7

et sont affectés au même point sur la sphère Bloch parce qu'ils sont égauxàphase mondiale. Algébriquement: où signifie « égale àphase mondiale ». Celasignifie qu'il y a un tel que . $|1\rangle$ $-|1\rangle$ $|1\rangle \equiv -|1\rangle$ $\equiv$ $\theta$ $-|1\rangle = e^{i \theta} |1\rangle$

$|0\rangle \equiv Z |0\rangle$ $|1\rangle \equiv Z |1\rangle$ $Z |+\rangle \not\equiv Z |+\rangle$ $|+\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$

Craig Gidney
la source

2

Selon Wikipedia , nous pouvons écrire n'importe quel état pur comme

| ψ ⟩ = \cos (\frac{θ}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{θ}{2}) | 1 ⟩

$|\psi\rangle = \cos\left( \frac{\theta}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\theta}{2} \right) |1 \rangle$

Où et sont les angles sur la sphère Bloch: $\theta$ $\phi$

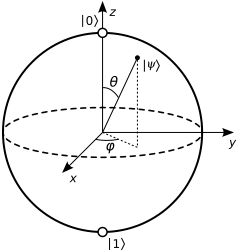
Presque tous les points de la surface (c'est-à-dire à l'état pur) ont une représentation unique en termes d'angles, à l'exception des pôles. Tout comme sur la Terre, le pôle Sud n'a pas de longitude bien définie (toute longitude fonctionne de la même manière), pour l'état , toute phase signifie la même chose. La "latitude" est ici , branchons cela dans l'équation: $|1 \rangle$ $\phi$ $\theta$ $\pi$

| 1 ⟩ = \cos (\frac{π}{2}) | 0 ⟩ + e^{i ϕ} \sin (\frac{π}{2}) | 1 ⟩ =

$|1\rangle = \cos\left( \frac{\pi}{2} \right) |0 \rangle + e^{i \phi} \sin\left( \frac{\pi}{2} \right) |1 \rangle =$

= 0 + e^{i ϕ} | 1 ⟩

$= 0 + e^{i \phi} |1 \rangle$

Si vous connaissez l'identité d'Euler, vous reconnaîtrez probablement comme une rotation dans le plan complexe. En particulier, puisque est une rotation pour , nous obtenons le fameux , pour arriver finalement à . $e^{i \phi}$ $Z$ $\phi = \pi$ $e^{i \pi} = -1$ $|1 \rangle = - |1 \rangle$

Norrius
la source

1

C'est faux. Écrire est trompeur: ce sont des états équivalents en ce qu'ils ne diffèrent que par une phase globale, mais cela ne signifie pas que les vecteurs d'état sont les mêmes. Vous obtenez ce résultat parce que vous supposez qu'il y a une bijection entre les vecteurs d'état et les points sur la sphère Bloch, ce qui n'est pas le cas. La bijection se situe entre les points de la sphère de Bloch et les états décrits comme des matrices de densité

| 1 ⟩ = - | 1 ⟩

$|1\rangle=-|1\rangle$

glS

@glS Merci, le qui en résulte semblait louche. Est-il judicieux d'améliorer cette réponse de votre point de vue, ou est-ce désespérément faux?

1 = - 1

$1=-1$

Norrius

c'est votre appel =). Je pense que la bonne réponse est celle donnée par DaftWullie (je pense que le demandeur avait une idée fausse similaire à celle de votre réponse). Je ne vois pas grand-chose à dire sur cette question

glS

Comment penser la porte Z dans une sphère Bloch?

Réponses: