Il est bien connu par le théorème de Ladner que si , alors il existe une infinité de problèmes -intermediate ( ). Il existe également des candidats naturels pour ce statut, tels que l'isomorphisme graphique, et un certain nombre d'autres, voir Problèmes entre P et NPC . Néanmoins, la grande majorité dans la foule des problèmes connus est connue pour être dans ou . Seule une petite fraction d'entre eux reste un candidat pour . En d'autres termes, si nous choisissons au hasard un naturel -problème parmi ceux connus, nous avons très peu de chance de choisir un candidat . Y a-t-il une explication à ce phénomène?
Je pourrais trouver 3 explications possibles, plus du côté philosophique:
La raison d'avoir une si petite fraction de naturelle candidats est que finira par se révéler vide. Je sais, cela implique , donc c'est très peu probable. Néanmoins, on pourrait toujours soutenir (bien que je ne sois pas l'un d'entre eux) que la rareté des problèmes naturels de est une observation empirique qui semble réellement soutenir , en revanche à la plupart des autres observations.
La petitesse de "natural- " représente une sorte de transition de phase nette entre des problèmes faciles et difficiles. Apparemment, les problèmes algorithmiques significatifs et naturels se comportent de manière à être faciles ou difficiles, la transition est étroite (mais existe toujours).
L'argument de 2 peut être poussé à l'extrême: finalement tous les problèmes dans "natural- " seront mis dans , mais , donc . Cela signifierait que tous les problèmes restants danssont "contre nature" (artificiel, sans signification réelle). Une interprétation de ceci pourrait être que les problèmes naturels sont soit faciles soit difficiles; la transition n'est qu'une construction logique, sans signification "physique". Cela rappelle quelque peu le cas des nombres irrationnels, qui sont parfaitement logiques, mais ne se présentent pas comme la valeur mesurée d'une quelconque grandeur physique. En tant que tels, ils ne viennent pas de la réalité physique, ils sont plutôt dans la «fermeture logique» de cette réalité.
Quelle explication préférez-vous ou pouvez-vous en suggérer une autre?
la source




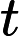
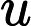





Réponses:
Comme d'autres l'ont souligné, il est discutable dans quelle mesure la chose que vous essayez d'expliquer est même vraie. On pourrait faire valoir que, dans les années 60 et 70, les informaticiens théoriques étaient simplement plus intéressés par les types de problèmes qui s'avèrent être soit en P, soit en NP-complet. Aujourd'hui, en raison de l'essor de la cryptographie théoriquement complexe, de l'informatique quantique, des réseaux, etc. - ainsi que du simple fait que l'exhaustivité de NP est devenue si bien comprise --- nous sommes de plus en plus intéressés par le genre de problèmes qui s'avèrent être NP-intermédiaires.
Pourtant, on pourrait se demander: dans la mesure où la chose est vraie --- c'est-à-dire, dans la mesure où tant de problèmes de recherche naturelle et d'optimisation "s'accrochent" à être NP-complet ou bien en P --- dans cette mesure , pourquoi est-ce vrai? Ici, je pense que vous pouvez obtenir beaucoup d'intuition en examinant un phénomène antérieur de la calculabilité: tant de modèles naturels de calcul "se cassent" pour être Turing-complet. Dans ce cas, je dirais que l'explication est que, une fois que vous avez quelques composants de base --- une mémoire de lecture / écriture, des boucles, des conditions, etc. - c'est difficile à éviterêtre capable de simuler une machine de Turing, et donc être Turing-complet. De la même manière, une fois que votre problème de recherche ou d'optimisation a quelques composants de base --- plus important encore, la possibilité de construire des "gadgets" qui imitent des portes logiques comme AND, OR et NOT --- il est difficile d'éviter de pouvoir pour coder SAT et donc être NP-complet.
De la façon dont j'aime y penser, des problèmes comme SAT exercent une puissante "attraction gravitationnelle" sur tous les autres problèmes de calcul dans leur voisinage, ce qui leur donne envie de "se casser" pour être NP-complet également. Donc, normalement, il ne nécessite même pas d'explication particulière lorsqu'un autre problème succombe à cette attraction! Ce qui est plus frappant, et qui a plus besoin d'explication, c'est quand un problème NP (apparemment) dur a une propriété qui lui permet de résister à l'attraction gravitationnelle de SAT. Nous voulons ensuite savoir: quelle est cette propriété? Pourquoi ne pouvez-vous pas jouer l'astuce de complétude NP habituelle pour ce problème, de construire des gadgets qui codent des portes logiques booléennes? J'ai fait une liste de quelques réponses courantes à cette question dans cette récente réponse CS.SE, mais (comme un autre intervenant l'a déjà souligné), il y a d'autres réponses possibles que j'ai manquées.
la source
De nombreux problèmes naturels peuvent être exprimés sous la forme de problèmes de satisfaction de contraintes, et il existe des théorèmes de dichotomie pour les CSP.
la source
Juste une blague: après avoir pensé à la "traction gravitationnelle SAT" dans la belle réponse de Scott Aaronson, une autre métaphore m'est venue à l'esprit: le sandwich 3-SAT 2-SAT !
... mais je ne sais pas si le sandwich peut être rempli d'ingrédients naturels (mais j'ai trouvé qu'il pouvait en être rempli - Sauce SAT [1] si l'hypothèse de temps exponentiel est vraie) :-D
Un autre résultat dans [1] est qu'il ne peut pas être rempli avec .







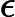




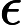


[1] Yunlei Zhao, Xiaotie Deng, CH Lee, Hong Zhu, -SAT and its properties







la source
Nous ne pouvons pas exclure une quatrième possibilité qu'il y ait beaucoup de problèmes intermédiaires naturels de . La rareté apparente est due au manque de techniques et d'outils nécessaires pour prouver le statut intermédiaire sous une conjecture de complexité plausible (Arora et Barak ont noté que nous ne pouvons pas prouver le statut intermédiaire de tout problème de naturel même en supposant ).N P N P N P P ≠ N P











Il semble que les vannes des problèmes intermédiaires de naturel sont ouvertes. Jonsson, Lagerkvist et Nordh ont étendu la technique de diagonalisation de Ladner, connue sous le nom de soufflage de trous dans les problèmes , et l'ont appliquée aux problèmes de satisfaction de contrainte. Ils ont obtenu un CSP qui est candidat pour le statut intermédiaire. Ils ont prouvé que le problème d'abduction propositionnelle a des fragments intermédiaires .N P N P





De plus, Grohe a prouvé l'existence de problèmes CSP intermédiaires supposant que . Il a obtenu de tels problèmes en restreignant la largeur d'arbre des graphiques primaires correspondants.F P T ≠ W [ 1 ]









Références :
1- M. Grohe. La complexité de l'homomorphisme et les problèmes de satisfaction des contraintes vus de l'autre côté. Journal de l'ACM, 54 (1), article 1, 2007
2- Peter Jonsson, Victor Lagerkvist et Gustav Nordh. Perçage de trous sous divers aspects des problèmes de calcul, avec des applications à la satisfaction des contraintes. Dans les actes de la 19e Conférence internationale sur les principes et la pratique de la programmation par contraintes (CP-2013). 2013.
la source
Voici un conte de fées sur la structure de Goldilocks des problèmes NP-intermédiaires. (Attention: cette histoire peut être une erreur utile pour générer et tester des hypothèses potentielles, mais elle n'est pas censée être scientifiquement rigoureuse. résolution, et la trichotomie heuristique de Terence Tao pour les problèmes. Consommer à vos risques et périls, comme avec toutes les concoctions agitant la main sur les mathématiques.)
Si presque toutes les instances d'un problème dans NP sont hautement structurées, alors le problème est en fait dans P. Les instances contiennent donc presque toutes beaucoup de redondance, et un algorithme à temps polynomial pour le problème est un moyen de prendre en compte la redondance. Il est même concevable que chaque problème dans P puisse être obtenu en prenant un problème dans EXP et en ajoutant une redondance structurée, via une certaine forme de remplissage (pas nécessairement le type habituel). S'il en était ainsi, alors un algorithme polynomial pourrait être considéré comme un moyen efficace d'annuler ce remplissage.
S'il y a suffisamment d'instances qui ne sont pas structurées, formant un "noyau de dureté", alors le problème est NP-complet.
Cependant, si ce "noyau de dureté" est trop clairsemé, alors il n'a que de la place pour représenter une partie du SAT, donc le problème est en P ou NP-intermédiaire. (Cet argument est l'essence du théorème de Ladner). Pour utiliser l'analogie de Scott, le «noyau de la dureté» exerce une attraction gravitationnelle sur le problème, pour qu'il soit NP-complet. Les instances du «noyau de dureté» ne contiennent pas beaucoup de redondance, et le seul algorithme réaliste qui fonctionne pour toutes ces instances est la recherche par force brute (bien sûr, s'il n'y en a qu'un nombre fini, la recherche de table fonctionne également).
De ce point de vue, les problèmes NP-intermédiaires devraient être rares dans la pratique, car ils nécessitent un équilibre fin de Boucle d'or entre des instances structurées et non structurées. Les instances devraient avoir suffisamment de redondance pour pouvoir être partiellement adaptées à un algorithme, mais il devrait y avoir suffisamment de noyau de dureté pour que le problème ne soit pas dans P.
On peut raconter une histoire encore plus simple (et amusante, mais aussi potentiellement encore plus trompeuse) basée sur des puzzles. Avec juste quelques contraintes, on peut forcer beaucoup de recherches à faire, par exemple NxN Sudoku est NP-complet. Pensez maintenant à être invité à résoudre de nombreux petits puzzles en une seule fois, en une seule fois (par exemple, de nombreux Sudokus 9x9). Le temps pris va être à peu près linéaire dans le nombre d'énigmes dans chaque instance, et ce problème est alors dans P. Pour les problèmes intermédiaires, on peut penser que chaque instance est un nombre important (mais pas trop grand) de Sudokus sur une grande (mais pas trop grandes) grilles. La raison pour laquelle nous n'observons pas beaucoup de ces problèmes est qu'ils seraient mornes à poser et à résoudre!
la source
Plusieurs réponses ont souligné que la prémisse de ma question (la rareté relative des candidats naturels ) pourrait être discutable. Après réflexion, je dois admettre qu’ils ont effectivement raison. En fait, on peut même aller aussi loin que de faire le cas qu'il ya effectivement plus naturel candidats que naturel problèmes COMPLETES. L'argument pourrait se présenter comme suit.N P I N PNPI NPI NP
Considérons le problème LOGCLIQUE, qui vise à décider si un graphe d'entrée -vertex a une clique de taille . Il s'agit d'un candidat naturel . Maintenant, le même type de "réduction d'échelle" peut être effectué sur n'importe quel problème -complete. Remplacez simplement la question "la chaîne d'entrée a-t-elle une propriété ?" par la question réduite " a-t-il une sous-chaîne de taille logarithmique qui a la propriété≥ log n N P I N P x Q x Q N P I P





NPI NP 
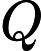

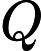
NPI P
De cette façon, nous pouvons construire un candidat naturel pour chaque problème naturel . En outre, il existe également des candidats génériques qui ne surviennent pas via une réduction d'échelle, tels que l'isomorphisme graphique, l'affacturage, etc. Ainsi, on peut en effet affirmer que "natural- " est en fait plus peuplé que "natural . "N P N P I N P CNPI NP NPI NPC
Bien sûr, ce processus de réduction d'échelle, en utilisant la belle métaphore de Scott, donne une raison évidente de résister à «l'attraction gravitationnelle» de SAT. Bien qu'il y ait des articles publiés sur LOGCLIQUE et des problèmes similaires, ils n'ont pas attiré trop d'attention, car ces problèmes sont moins excitants que les candidats génériques , où il n'y a pas de compréhension claire de la façon dont l'attirance gravitationnelle est résistée, sans tomber dans .PNPI P
la source