Analyse des amplis opérationnels: quand les «règles de rétroaction négative» s'appliquent-elles?

9

Lorsque nous construisons des circuits d'amplificateurs opérationnels qui utilisent une rétroaction négative, comme ceci:

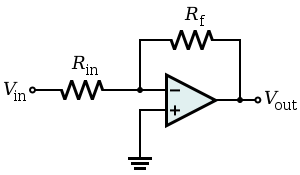
... nous pouvons analyser le circuit très facilement, en supposant que raison d'une rétroaction négative (en supposant également que l'ampli op est idéal, bien sûr).

v^{-} = v^{+}

$v^- = v^+$

Outre les cas évidents de haute précision où ces modèles simplifiés tombent en panne, quand est-ce et quand n'est-ce pas valable?
Par exemple, si nous remplaçons la résistance de rétroaction par un autre élément - peut-être un condensateur, une inductance, une diode (diode au silicium ordinaire, diode Zener, etc.), ou une combinaison d'entre eux et d'autres éléments de circuit communs - comment savons-nous où cela la simplification est valable?
De plus, même si nous restons avec une résistance comme élément de rétroaction, car la résistance devient très, très élevée, à un moment donné, nous pouvons à peu près la considérer comme un circuit ouvert, et donc clairement ce modèle tombe en panne quelque part en cours de route.

La question est donc: sous quelles contraintes cette approximation est-elle "assez vraie" pour donner des résultats utiles?

ÉDITER:

Pour un autre exemple, considérons le circuit amplificateur de journal inverseur de base:

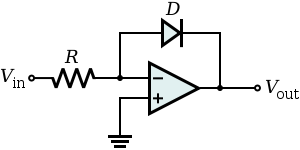
Si nous résolvons l'équation de la diode Shockley

{je}_{ré} = {je}_{S} (e^{v ré / V T} - 1)

$i_D = I_S(e^{vD/VT} - 1)$

pour vD, nous obtenons (en ignorant le 1, ce qui n'est généralement pas pertinent car l'exponentielle sera plutôt énorme)

v_{ré} = V T \ln (\frac{{je}_{ré}}{{je}_{S}})

$v_D = VT \ln{\left(\frac{i_D}{I_S} \right)}$

Si nous utilisons ensuite la méthode virtuelle courte pour voir que nous obtenons l'expression correcte pour la sortie:

{je}_{ré} = \frac{v_{je n} - 0}{R_{je n}}

$i_D = \frac{v_{in} - 0}{R_{in}}$

v_{o u t} = - V T \cdot \ln (\frac{v_{je n}}{{je}_{S} R_{je n}})

$v_{out} = -VT \cdot \ln{\left( \frac{v_{in}}{I_S R_{in}} \right)}$

Ainsi, la méthode virtuelle courte fonctionne ici. Mais puisque cette diode sera un circuit ouvert lorsque je ne sais pas comment déterminer à l' avance que l'analyse sera valide.

v_{o u t} > v^{-}

$v_{out} > v^-$

operational-amplifier negative feedback constraints exscape
la source

Avec un ampli-op idéal, les bornes +et -seront égales indépendamment de l'utilisation de l'ampli-op dans un circuit.

kevlar1818

2

@ kevlar1818 Comment cela fonctionnerait-il? S'il n'y a pas de connexion entre la sortie et les entrées, comment pourrait-il éventuellement changer les entrées?

exscape

Voir ma réponse pour des éclaircissements.

kevlar1818

@ kevlar1818: L'hypothèse que les entrées de l'ampli op seront égales dépend dans une certaine mesure non seulement de l'ampli op étant idéal, mais aussi des autres composants du circuit. Si d'autres composants du circuit font que la dérivée première de la tension du chemin de rétroaction par rapport à la tension de sortie est nulle (comme cela pourrait arriver s'il y a un retard RC non compensé), l'ampli op ne serait pas en mesure d'équilibrer instantanément les entrées en réponse à un stimulus pas à pas.

supercat

7

Comme vous l'avez dit, le fait que les deux entrées opamp soient presque égales est une simplification et dépend de paramètres souvent non explicites. C'est une bonne question dans la mesure où il est essentiel de connaître les limites de tous les raccourcis ou règles empiriques que vous utilisez.

Comme clabacchio l'a déjà dit, un endroit où les hypothèses sont violées est si la sortie de l'ampli op est écrêtée, ou devrait dépasser sa plage disponible pour émettre le signal souhaité. D'autres raisons qui rendent l'hypothèse non valide comprennent:

La rétroaction n'est pas négative. Cela peut sembler stupide, mais j'ai en fait montré à quelqu'un un simple circuit d'hystérésis opamp dans une interview et leur ai demandé de tracer un tracé de la tension de sortie en fonction de la tension d'entrée. Plus d'un candidat a commencé en disant que l'opamp tenterait de garder ses deux entrées identiques, puis s'est enfoncé dans un trou plus profond à partir de là. Inutile de dire qu'il s'agissait de courtes interviews.
Le gain n'est pas suffisant. Notez que la règle de maintenir les entrées égales suppose un gain infini. De même, la règle selon laquelle Gain = -Rf / Rin suppose un gain infini. Normalement, les gains en boucle ouverte opamp sont d'environ 100k ou plus et nous ne demandons pas plus de 100 ou peut-être 1000 au plus à partir d'une seule étape, il semblerait donc que ce soit un petit problème.

Cependant, cela oublie l'effet de la fréquence sur le gain. Un ampli op de 1 MHz peut être spécifié pour un gain de tension en boucle ouverte de 100k à DC, mais si vous l'utilisez pour l'audio et que vous souhaitez passer à 20 kHz, alors vous n'avez qu'un gain en boucle ouverte de 50 cas le plus défavorable. Si vous réglez les résistances de rétroaction pour un gain de 25, cela ne laisse que 2 fois la marge à l'extrémité supérieure, ce qui réduira considérablement le gain en boucle fermée aux hautes fréquences.
Limitation du taux de balayage. Même avec un gain suffisant et une rétroaction appropriée, l'ampli-op ne peut que changer sa sortie si rapidement. C'est à cela que sert la spécification du taux de balayage. Le produit gain * de bande passante est destiné aux petits signaux. Les signaux de grande amplitude peuvent rencontrer des problèmes de vitesse de balayage. Pour la plupart des amplis-op, le signal de sortie de swing complet est une fréquence plutôt inférieure à ce que le produit de gain de bande passante impliquait.

Olin Lathrop
la source

Bonne réponse. J'ai supposé que l'ampli op était idéal, car sinon l'hyphothesis est toujours faux :)

clabacchio

4

Tant que l'ampli-op peut régler les entrées égales en entraînant la sortie à une certaine tension, ce sera le cas.

Cette hypothèse tombe lorsqu'elle ne peut pas, comme si elle a un circuit ouvert dans la rétroaction (positive ou négative). Ensuite, il saturera l'un des rails, selon l'entrée la plus élevée. Notez que la rétroaction en circuit ouvert peut également être une diode inversée.

Un autre cas peut se présenter si la tension qui permet l'équilibre aux entrées est au-delà des tensions de saturation. Encore une fois, l'ampli op saturera et l'entrée sera déséquilibrée.

Mais pourquoi les entrées doivent-elles être égales?

L'ampli op a trois régions de fonctionnement, une appelée région à gain élevé et deux régions de saturation . La règle selon laquelle les entrées doivent être égales ne s'applique qu'à la région à gain élevé et vient du fait que pour l'ampli-op idéal:

V_{o u t} = \infty (V_{ré}) = \infty (V_{+} - V_{-})

$V_{out} = \infty (V_d) = \infty (V_+ - V_-)$

ce qui signifie que la tension de sortie n'est finie que si les tensions d'entrée sont égales, donc l'ampli-op force la tension de sortie à la valeur qui met à zéro la différence.

Quand l'ampli op sature, cependant, la tension de sortie est juste donnée par

V_{o u t} = V_{s une t}

$V_{out} = V_{sat}$

ce qui signifie que l'ampli op fait de son mieux pour régler les entrées égales, mais il se heurte à un mur amovible. Ainsi, les entrées peuvent déséquilibrer pour satisfaire la tension de sortie.

Dans votre exemple, vous pouvez constater que l'ampli opérationnel sature lorsque l'entrée est égale ou supérieure à:

V_{je n}^{S UNE T -} = - V_{S UNE T -} \frac{R_{je n}}{R_{F}}

$V_{in}^{SAT-} = - V_{SAT-}\frac{R_{in}}{R_{f}}$

Dans votre exemple de circuit, lorsque Vin est négatif, V + sera plus élevé, puis la sortie sera saturée. Il n'y a donc aucun moyen pour la rétroaction de rétablir l'équilibre, car la diode sera inversée, donc pour chaque entrée négative, la sortie sera la tension de saturation.

clabacchio
la source

Merci, mais je savais déjà la plupart de cela (j'ai analysé des tonnes de différents circuits d'amplificateurs opérationnels, mais ils avaient tous une chose en commun: il était généralement évident que cette méthode s'appliquerait ou non). Je suppose que je suis confus à propos de ce qui compte comme un circuit ouvert - par exemple, une diode peut en être une (idéale, au moins), mais la méthode semble toujours fonctionner là-bas. J'ai ajouté l'exemple de l'ampli log.

départ le

Je viens de me souvenir de toi dans ces vieux jours! Je suis curieux au sujet de la formule de saturation (la dernière. Pourriez-vous me donner une référence à cette formule, au lieu de vous demander d'en parler davantage.

hbak

2

Dans cette réponse, je fais la dérivation de la fonction de transfert et je conclus par pourquoi nous pouvons supposer que les deux entrées sont égales.

Il y a une simplification mineure dans le calcul, qui est pardonnable si le gain en boucle ouverte est très élevé. Cela est vrai pour la plupart des opamps, j'ai utilisé le chiffre 100 000.

$\times$

stevenvh
la source

Analyse des amplis opérationnels: quand les «règles de rétroaction négative» s'appliquent-elles?

Réponses:

Mais pourquoi les entrées doivent-elles être égales?