Quel est l'algorithme de tri le plus obscur que vous connaissez? [fermé]

Je viens de lire sur cyclesort via un article de blog sortvis.org. C'est probablement le plus obscur dont j'ai entendu parler jusqu'à présent, car il utilise des mathématiques que je ne connais pas (détection des cycles dans les permutations d'ensembles entiers).

Quel est le plus obscur que vous connaissez?

Avez-vous déjà entendu parler du tri Patience ? Eh bien maintenant vous avez ...

Slowsort fonctionne en multipliant et en abandonnant (par opposition à diviser pour mieux régner). C'est intéressant car c'est sans doute l'algorithme de tri le moins efficace qui puisse être construit (asymptotiquement, et avec la restriction qu'un tel algorithme, tout en étant lent, doit toujours tout le temps viser un résultat).

Cela le compense de bogosort car dans le meilleur des cas, bogosort est assez efficace - à savoir, lorsque le tableau est déjà trié. Slowsort ne «souffre» pas d'un tel comportement dans le meilleur des cas. Même dans son meilleur cas, il a toujours un temps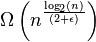 d' exécution pour ϵ > 0.

Voici son pseudocode, adapté de l'article allemand Wikipédia :

function slowsort(A, i, j):
  if i >= j: return

  m = (i + j) / 2
  slowsort(A, i, m)
  slowsort(A, m + 1, j)

  if A[j] < A[m]:
    swap(A[j], A[m])

  slowsort(A, i, j - 1)

Je ne sais pas si cela compte comme obscur, mais Bogosort est l'un des "algorithmes" de tri les plus ridicules . Les liens de la page Bogosort sont également amusants.

Et il y a ce joyau de la section sur "le bogo-tri quantique".

On peut dire que la création d' univers 2 ^N est également très gourmande en mémoire.

Hmmm ... on pourrait dire ça :-).

Un autre "algorithme" obscur est le tri de conception intelligent - mais aucun algorithme n'est plus rapide ou consomme moins de mémoire :)

Sleep Sort est plutôt nouveau.

    #!/bin/bash
    function f() {
        sleep "$1"
        echo "$1"
    }
    while [ -n "$1" ]
    do
        f "$1" &
        shift
    done
    wait

exemple d'utilisation:

    ./sleepsort.bash 5 3 6 3 6 3 1 4 7

Je pense que le type de bulle serait également la mauvaise réponse dans cette situation

:)

Knuth Volume 3 ¹ , dans la réponse à l'un des exercices, donne une implémentation d'un algorithme de tri sans nom qui est essentiellement un ancien code de golf - le tri le plus court que vous puissiez écrire en langage d'assemblage MIX. Le code court vient au prix oh-si-mineur de la complexité O (N ³ ) ...

¹ Au moins dans les anciennes éditions. Compte tenu des modifications apportées à MIXAL pour la nouvelle édition, je ne sais pas s'il est toujours là, ou même fait le petit peu de sens dans le MIXAL d'origine.

Pour ma classe de structures de données, j'ai dû (explicitement) prouver l'exactitude du tri Stooge . Il a un temps d'exécution de O (n ^ {log 3 / log 1.5}) = O (n ^ 2.7095 ...).

Je ne sais pas si c'est le plus obscur, mais le type de spaghetti est l'un des meilleurs dans les situations où vous pouvez l'utiliser.

Un des livres originaux de Knuth, "Tri et recherche", comportait un volet central qui schématisait un processus qui triait un fichier sur bande sans disque dur. Je pense qu'il a utilisé six lecteurs de bande et a montré explicitement quand chacun était lu en avant, en arrière, en rembobinage ou en veille. Aujourd'hui, c'est un monument à une technologie obsolète.

J'ai fait une fois un tri à bulles dans les registres vectoriels dans l'assembleur CRAY. La machine avait une instruction de double décalage, qui vous permettait de déplacer le contenu d'un registre vectoriel vers le haut / bas d'un mot. Mettez le point sur deux dans deux registres vectoriels, puis vous pourriez faire un tri complet des bulles sans avoir à faire une autre référence de mémoire jusqu'à ce que vous ayez terminé. À l'exception de la nature N ** 2 du tri à bulles, il était efficace.

J'ai également eu besoin de faire une sorte de virgule flottante d'un vecteur de longueur 4 aussi rapidement que possible pour une seule sorte. Est-ce par recherche de table (le bit de signe de A2-A1 est un bit, le signe de A3-A1 forme un autre bit ..., puis vous recherchez le vecteur de permutation dans une table. C'était en fait la solution la plus rapide que j'ai pu trouver avec. Ne fonctionne pas bien sur les architectures modernes cependant, les unités flottantes et entières sont trop séparées.

Google Code Jam a eu un problème avec un algorithme appelé Gorosort, que je pense qu'ils ont inventé pour le problème.

Goro a 4 bras. Goro est très fort. Tu ne plaisantes pas avec Goro. Goro doit trier un tableau de N entiers différents. Les algorithmes ne sont pas la force de Goro; la force est la force de Goro. Le plan de Goro est d'utiliser les doigts sur deux de ses mains pour maintenir plusieurs éléments du tableau et frapper la table avec ses troisième et quatrième poings aussi fort que possible. Cela fera voler les éléments non sécurisés du réseau dans les airs, les mélanger au hasard et retomber dans les emplacements vides du réseau.

http://code.google.com/codejam/contest/dashboard?c=975485#s=p3

Je ne me souviens pas du nom, mais c'était essentiellement

while Array not sorted

  rearrange the array in a random order

Tri par coque

Peut-être que l'algorithme lui-même n'est pas si obscur, mais qui peut nommer une implémentation réellement utilisée dans la pratique? Je peux!

TIGCC (un compilateur basé sur GCC pour les calculatrices graphiques TI-89/92 / V200) utilise le tri Shell pour l' qsortimplémentation dans sa bibliothèque standard:

__ATTR_LIB_C__ void qsort(void *list, short num_items, short size, compare_t cmp_func)
{
  unsigned short gap,byte_gap,i,j;                
  char *p,*a,*b,temp;                       
  for (gap=((unsigned short)num_items)>>1; gap>0; gap>>=1)    // Yes, this is not a quicksort,
    {                                                         // but works fast enough...    
      byte_gap=gap*(unsigned short)size;
      for(i=byte_gap; i<((unsigned short)num_items)*(unsigned short)size; i+=size)
        for(p=(char*)list+i-byte_gap; p>=(char*)list; p-= byte_gap)
          {
            a=p; b=p+byte_gap;
            if(cmp_func(a,b)<=0) break;
            for(j=size;j;j--)
              temp=*a, *a++=*b, *b++=temp;
          }
    }
}

Le tri du shell a été choisi en faveur de quicksort pour maintenir une taille de code faible. Bien que sa complexité asymptotique soit pire, la TI-89 n'a pas beaucoup de RAM (190K, moins la taille du programme et la taille totale des variables non archivées), il est donc assez sûr de supposer que le nombre d'éléments au dessous de.

Une implémentation plus rapide a été écrite après que je me sois plaint d'être trop lent dans un programme que j'écrivais. Il utilise de meilleures tailles d'espace, ainsi que des optimisations d'assemblage. Il peut être trouvé ici: qsort.c