Comment pourrais-je générer une liste de toutes les permutations possibles d'une chaîne entre les caractères x et y de longueur, contenant une liste variable de caractères.
N'importe quelle langue fonctionnerait, mais elle devrait être portable.
string
language-agnostic
cross-platform
UnkwnTech
la source
la source

Réponses:
Il y a plusieurs moyens de le faire. Les méthodes courantes utilisent la récursivité, la mémorisation ou la programmation dynamique. L'idée de base est de produire une liste de toutes les chaînes de longueur 1, puis à chaque itération, pour toutes les chaînes produites dans la dernière itération, ajoutez cette chaîne concaténée avec chaque caractère de la chaîne individuellement. (l'index de variable dans le code ci-dessous garde une trace du début de la dernière et de la prochaine itération)
Quelques pseudocodes:
vous devrez alors supprimer toutes les chaînes de moins de x de longueur, ce seront les premières entrées (x-1) * len (originalString) de la liste.
la source
Il vaut mieux utiliser le retour en arrière
la source
Vous allez avoir beaucoup de cordes, c'est sûr ...
Où x et y sont la façon dont vous les définissez et r est le nombre de caractères que nous sélectionnons - si je vous comprends bien. Vous devez absolument les générer au besoin et ne pas être bâclé et dire, générer un ensemble de pouvoirs, puis filtrer la longueur des chaînes.
Ce qui suit n'est certainement pas la meilleure façon de les générer, mais c'est néanmoins un aparté intéressant.
Knuth (volume 4, fascicule 2, 7.2.1.3) nous dit que la combinaison (s, t) équivaut à s + 1 choses prises t à la fois avec répétition - une combinaison (s, t) est la notation utilisée par Knuth qui est égal à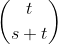 . Nous pouvons comprendre cela en générant d'abord chaque combinaison (s, t) sous forme binaire (donc, de longueur (s + t)) et en comptant le nombre de 0 à gauche de chaque 1.
. Nous pouvons comprendre cela en générant d'abord chaque combinaison (s, t) sous forme binaire (donc, de longueur (s + t)) et en comptant le nombre de 0 à gauche de chaque 1.
10001000011101 -> devient la permutation: {0, 3, 4, 4, 4, 1}
la source
Solution non récursive selon Knuth, exemple Python:
la source
"54321"seulement UNE chaîne est montré (lui - même).nextPermutation()est intéressant, c'est qu'il est sans état - il suffit de l'entrée pour permuter et les index ne sont pas conservés d'une itération à l'autre. Il est capable de le faire en supposant que l'entrée initiale a été triée et en trouvant des index (k0etl0) elle-même, en fonction de l'endroit où l'ordre est conservé. Le tri d'une entrée comme "54321" -> "12345" permettrait à cet algorithme de trouver toutes les permutations attendues. Mais comme cela fait beaucoup de travail supplémentaire pour retrouver ces index pour chaque permutation qu'il génère, il existe des moyens plus efficaces de le faire de manière non récursive.Vous pouvez consulter « Énumération efficace des sous-ensembles d'un ensemble », qui décrit un algorithme pour faire une partie de ce que vous voulez - générer rapidement tous les sous-ensembles de N caractères de longueur x à y. Il contient une implémentation en C.
Pour chaque sous-ensemble, vous devrez toujours générer toutes les permutations. Par exemple, si vous vouliez 3 caractères de "abcde", cet algorithme vous donnerait "abc", "abd", "abe" ... mais vous devrez permuter chacun pour obtenir "acb", "bac", "bca", etc.
la source
Un code Java fonctionnel basé sur la réponse de Sarp :
la source
Voici une solution simple en C #.
Il ne génère que les permutations distinctes d'une chaîne donnée.
la source
Il y a beaucoup de bonnes réponses ici. Je propose également une solution récursive très simple en C ++.
Remarque : les chaînes avec des caractères répétés ne produiront pas de permutations uniques.
la source
Je viens de fouetter cela rapidement dans Ruby:
Vous pourriez vous pencher sur l'API de langage pour les fonctions de type permutation intégrées, et vous pourrez peut-être écrire du code plus optimisé, mais si les nombres sont si élevés, je ne suis pas sûr qu'il existe un moyen de contourner beaucoup de résultats .
Quoi qu'il en soit, l'idée derrière le code est de commencer par une chaîne de longueur 0, puis de garder une trace de toutes les chaînes de longueur Z où Z est la taille actuelle dans l'itération. Ensuite, parcourez chaque chaîne et ajoutez chaque caractère à chaque chaîne. Enfin, à la fin, supprimez tous ceux qui étaient en dessous du seuil x et renvoyez le résultat.
Je ne l'ai pas testé avec une entrée potentiellement dénuée de sens (liste de caractères nuls, valeurs étranges de x et y, etc.).
la source
Ceci est une traduction de la version Ruby de Mike, en Common Lisp:
Et une autre version, légèrement plus courte et utilisant plus de fonctionnalités de boucle:
la source
Voici une solution récursive C # avec un mot simple:
Méthode:
Appel:
la source
... et voici la version C:
la source
Imprime toutes les permutations sans doublons
la source
Solution récursive en C ++
la source
En Perl, si vous souhaitez vous limiter à l'alphabet en minuscules, vous pouvez le faire:
Cela donne toutes les chaînes possibles entre 1 et 4 caractères en utilisant des caractères minuscules. Pour les majuscules, changez
"a"en"A"et"zzzz"en"ZZZZ".Pour les cas mixtes, cela devient beaucoup plus difficile, et probablement impossible avec l'un des opérateurs intégrés de Perl comme celui-là.
la source
Réponse Ruby qui fonctionne:
la source
la source
La récursivité Java suivante imprime toutes les permutations d'une chaîne donnée:
Voici la version mise à jour de la méthode "permut" ci-dessus qui fait n! (n factoriel) moins d'appels récursifs par rapport à la méthode ci-dessus
la source
Je ne sais pas pourquoi vous voudriez faire cela en premier lieu. L'ensemble résultant pour toutes les valeurs modérément grandes de x et y sera énorme et augmentera de façon exponentielle à mesure que x et / ou y deviendront plus grands.
Disons que votre jeu de caractères possibles est constitué des 26 lettres minuscules de l'alphabet, et vous demandez à votre application de générer toutes les permutations où longueur = 5. En supposant que vous ne manquez pas de mémoire, vous obtiendrez 11 881 376 (soit 26 au pouvoir) de 5) cordes en arrière. Augmentez cette longueur jusqu'à 6, et vous obtiendrez 308 915 776 cordes. Ces chiffres deviennent extrêmement élevés, très rapidement.
Voici une solution que j'ai mise en place en Java. Vous devrez fournir deux arguments d'exécution (correspondant à x et y). S'amuser.
la source
Voici une version non récursive que j'ai imaginée, en javascript. Il n'est pas basé sur celui non récursif de Knuth ci-dessus, bien qu'il présente certaines similitudes dans l'échange d'éléments. J'ai vérifié son exactitude pour les tableaux d'entrée jusqu'à 8 éléments.
Une optimisation rapide consisterait à pré-voler la
outbaie et à éviterpush().L'idée de base est:
Étant donné un tableau source unique, générez un premier nouvel ensemble de tableaux qui permutent le premier élément avec chaque élément suivant à tour de rôle, en laissant à chaque fois les autres éléments inchangés. par exemple: donné 1234, génère 1234, 2134, 3214, 4231.
Utilisez chaque tableau de la passe précédente comme base pour une nouvelle passe, mais au lieu d'échanger le premier élément, remplacez le deuxième élément par chaque élément suivant. De plus, cette fois, n'incluez pas le tableau d'origine dans la sortie.
Répétez l'étape 2 jusqu'à ce que vous ayez terminé.
Voici l'exemple de code:
la source
En rubis:
C'est assez rapide, mais ça va prendre du temps =). Bien sûr, vous pouvez commencer par "aaaaaaaa" si les chaînes courtes ne vous intéressent pas.
J'aurais peut-être mal interprété la question réelle - dans l'un des articles, cela semblait comme si vous aviez juste besoin d'une bibliothèque de chaînes bruteforce, mais dans la question principale, il semble que vous deviez permuter une chaîne particulière.
Votre problème est un peu similaire à celui-ci: http://beust.com/weblog/archives/000491.html (listez tous les nombres entiers dans lesquels aucun des chiffres ne se répète, ce qui a abouti à un grand nombre de langues le résolvant, avec le ocaml guy utilisant des permutations, et certains gars java utilisant encore une autre solution).
la source
J'en avais besoin aujourd'hui, et bien que les réponses déjà données m'ont pointé dans la bonne direction, elles n'étaient pas tout à fait ce que je voulais.
Voici une implémentation utilisant la méthode de Heap. La longueur du tableau doit être d'au moins 3 et pour des raisons pratiques, pas plus de 10 ou plus, selon ce que vous voulez faire, la patience et la vitesse d'horloge.
Avant d'entrer dans votre boucle, initialisez
Perm(1 To N)avec la première permutation,Stack(3 To N)avec des zéros * etLevelavec2**. À la fin de l'appel en boucleNextPerm, qui retournera false lorsque nous aurons terminé.* VB le fera pour vous.
** Vous pouvez modifier un peu NextPerm pour rendre cela inutile, mais c'est plus clair comme ça.
D'autres méthodes sont décrites par divers auteurs. Knuth en décrit deux, l'un donne un ordre lexical, mais est complexe et lent, l'autre est connu comme la méthode des changements simples. Jie Gao et Dianjun Wang ont également écrit un article intéressant.
la source
Ce code en python, lorsqu'il est appelé avec
allowed_charactersset to[0,1]et 4 caractères max, générerait 2 ^ 4 résultats:['0000', '0001', '0010', '0011', '0100', '0101', '0110', '0111', '1000', '1001', '1010', '1011', '1100', '1101', '1110', '1111']J'espère que cela vous sera utile. Fonctionne avec n'importe quel caractère, pas seulement des nombres
la source
Voici un lien qui décrit comment imprimer les permutations d'une chaîne. http://nipun-linuxtips.blogspot.in/2012/11/print-all-permutations-of-characters-in.html
la source
Bien que cela ne réponde pas exactement à votre question, voici une façon de générer chaque permutation des lettres à partir d'un certain nombre de chaînes de même longueur: par exemple, si vos mots étaient "café", "joomla" et "moodle", vous pouvez attendez-vous à une sortie comme "coodle", "joodee", "joffle", etc.
Fondamentalement, le nombre de combinaisons est le (nombre de mots) à la puissance de (nombre de lettres par mot). Alors, choisissez un nombre aléatoire entre 0 et le nombre de combinaisons - 1, convertissez ce nombre en base (nombre de mots), puis utilisez chaque chiffre de ce nombre comme indicateur du mot à partir duquel prendre la lettre suivante.
par exemple: dans l'exemple ci-dessus. 3 mots, 6 lettres = 729 combinaisons. Choisissez un nombre aléatoire: 465. Convertissez en base 3: 122020. Prenez la première lettre du mot 1, la deuxième du mot 2, la troisième du mot 2, la quatrième du mot 0 ... et vous obtenez ... "joofle".
Si vous vouliez toutes les permutations, faites une boucle de 0 à 728. Bien sûr, si vous ne choisissez qu'une seule valeur aléatoire, une manière beaucoup
plus simple etmoins déroutante serait de parcourir les lettres. Cette méthode vous permet d'éviter la récursivité, si vous voulez toutes les permutations, et vous donne l'impression de connaître Maths (tm) !Si le nombre de combinaisons est excessif, vous pouvez le diviser en une série de mots plus petits et les concaténer à la fin.
la source
c # itératif:
la source
la source
Voici mon point de vue sur une version non récursive
la source
La solution pythonique:
la source
Eh bien, voici une solution élégante, non récursive, O (n!):
la source