Je me prépare actuellement pour une interview, et cela m'a rappelé une question qui m'a été posée une fois lors d'une interview précédente qui ressemblait à ceci:
"On vous a demandé de concevoir un logiciel pour afficher en permanence les 10 principaux termes de recherche sur Google. Vous avez accès à un flux qui fournit un flux sans fin en temps réel de termes de recherche actuellement recherchés sur Google. Décrivez quels algorithmes et structures de données vous utiliseriez pour l'implémenter. Vous devez concevoir deux variantes:
(i) Affichez les 10 principaux termes de recherche de tous les temps (c'est-à-dire depuis que vous avez commencé à lire le flux).
(ii) N'afficher que les 10 principaux termes de recherche du mois dernier, mis à jour toutes les heures.
Vous pouvez utiliser une approximation pour obtenir la liste des 10 premiers, mais vous devez justifier vos choix. »
J'ai bombardé dans cette interview et je ne sais toujours pas vraiment comment mettre en œuvre cela.
La première partie demande les 10 éléments les plus fréquents dans une sous-séquence en croissance continue d'une liste infinie. J'ai examiné les algorithmes de sélection, mais je n'ai trouvé aucune version en ligne pour résoudre ce problème.
La deuxième partie utilise une liste finie, mais en raison de la grande quantité de données en cours de traitement, vous ne pouvez pas vraiment stocker tout le mois de termes de recherche en mémoire et calculer un histogramme toutes les heures.
Le problème est rendu plus difficile par le fait que la liste des 10 premiers est constamment mise à jour, vous devez donc calculer votre top 10 sur une fenêtre glissante.
Des idées?

what is the most frequent item in the subsequence [2; 2; 3; 3; 3; 4; 4; 4; 4; 5; 5] of your sequence?Réponses:
Eh bien, cela ressemble à une énorme quantité de données, avec un coût peut-être prohibitif pour stocker toutes les fréquences. Lorsque la quantité de données est si grande que nous ne pouvons pas espérer tout stocker, nous entrons dans le domaine des algorithmes de flux de données .
Livre utile dans ce domaine: Muthukrishnan - "Flux de données: algorithmes et applications"
Référence étroitement liée au problème actuel que j'ai choisi parmi les éléments ci-dessus: Manku, Motwani - "Approximate Frequency Counts over Data Streams" [pdf]
À propos, Motwani, de Stanford, (modifier) était un auteur du très important livre "Algorithmes aléatoires" .
Le 11e chapitre de ce livre traite de ce problème. Edit: Désolé, mauvaise référence, ce chapitre particulier est sur un problème différent. Après vérification, je recommande plutôt la section 5.1.2 du livre de Muthukrishnan , disponible en ligne.Heh, belle question d'entretien.
la source
Aperçu de l'estimation de fréquence
Il existe des algorithmes bien connus qui peuvent fournir des estimations de fréquence pour un tel flux en utilisant une quantité de stockage fixe. L'un est Fréquent, par Misra et Gries (1982). À partir d'une liste de n éléments, il trouve tous les éléments qui se produisent plus de n / k fois, en utilisant des compteurs k - 1 . Ceci est une généralisation de Boyer et Moore majorité algorithme (Fischer-Salzberg, 1982), où k est 2. Manku et de Motwani de LossyCounting (2002) et de Metwally de peu encombrant algorithmes (2005) ont des exigences d'espace similaires, mais peuvent fournir des estimations plus précises sous certaines conditions.
La chose importante à retenir est que ces algorithmes ne peuvent fournir que des estimations de fréquence. Plus précisément, l'estimation de Misra-Gries peut sous-estimer la fréquence réelle de (n / k) éléments.
Supposons que vous disposiez d'un algorithme capable d'identifier positivement un élément uniquement s'il se produit plus de 50% du temps. Alimentez cet algorithme un flux de N éléments distincts, puis ajoutez N - 1 copies supplémentaires d'un élément, x , pour un total de 2N - 1 éléments. Si l'algorithme vous indique que x dépasse 50% du total, il doit avoir été dans le premier flux; si ce n'est pas le cas, x n'était pas dans le flux initial. Pour que l'algorithme puisse effectuer cette détermination, il doit stocker le flux initial (ou un résumé proportionnel à sa longueur)! Ainsi, nous pouvons nous prouver que l'espace requis par un tel algorithme "exact" serait Ω ( N ).
Au lieu de cela, ces algorithmes de fréquence décrits ici fournissent une estimation, identifiant tout élément qui dépasse le seuil, ainsi que certains éléments qui tombent en dessous de celui-ci d'une certaine marge. Par exemple, l' algorithme Majority , utilisant un seul compteur, donnera toujours un résultat; si un élément dépasse 50% du flux, il sera trouvé. Mais cela peut également vous donner un élément qui n'apparaît qu'une seule fois. Vous ne le sauriez pas sans faire un deuxième passage sur les données (en utilisant, encore une fois, un seul compteur, mais en ne recherchant que cet élément).
L'algorithme fréquent
Voici une description simple de l' algorithme Frequent de Misra-Gries . Demaine (2002) et d'autres ont optimisé l'algorithme, mais cela vous donne l'essentiel.
Spécifiez la fraction seuil, 1 / k ; tout élément qui se produit plus de n / k fois sera trouvé. Créez une carte vide (comme un arbre rouge-noir); les clés seront des termes de recherche et les valeurs seront un compteur pour ce terme.
Notez que vous pouvez traiter une quantité infinie de données avec une quantité de stockage fixe (uniquement la carte de taille fixe). La quantité de stockage requise dépend uniquement du seuil d'intérêt et la taille du flux n'a pas d'importance.
Comptage des recherches
Dans ce contexte, vous pouvez peut-être tamponner une heure de recherche et effectuer ce processus sur les données de cette heure. Si vous pouvez effectuer un deuxième passage sur le journal de recherche de cette heure, vous pouvez obtenir un décompte exact des occurrences des meilleurs "candidats" identifiés lors du premier passage. Ou, peut-être qu'il est normal de faire un seul passage et de signaler tous les candidats, sachant que tout élément qui devrait être là est inclus, et que tous les extras ne sont que du bruit qui disparaîtra dans l'heure qui suit.
Tous les candidats qui dépassent vraiment le seuil d'intérêt sont stockés sous forme de résumé. Conservez la valeur d'un mois de ces résumés, en jetant le plus ancien chaque heure, et vous obtiendrez une bonne approximation des termes de recherche les plus courants.
la source
C'est l'un des projets de recherche que je vis actuellement. L'exigence est presque exactement la vôtre, et nous avons développé de beaux algorithmes pour résoudre le problème.
L'entrée
L'entrée est un flux infini de mots ou de phrases anglais (nous les appelons
tokens).Le résultat
Une application de cette recherche est de trouver le sujet brûlant ou les tendances du sujet sur Twitter ou Facebook. Nous avons un robot d'exploration qui parcourt le site Web, ce qui génère un flux de mots, qui alimentera le système. Le système sortira alors les mots ou les phrases de fréquence la plus élevée, soit globalement, soit historiquement. Imaginez au cours des dernières semaines que l'expression «Coupe du monde» apparaîtra plusieurs fois sur Twitter. Il en va de même pour "Paul le poulpe". :)
Chaîne en nombres entiers
Le système a un identifiant entier pour chaque mot. Bien qu'il existe une infinité de mots possibles sur Internet, mais après avoir accumulé un grand nombre de mots, la possibilité de trouver de nouveaux mots devient de plus en plus faible. Nous avons déjà trouvé 4 millions de mots différents et attribué un identifiant unique à chacun. Cet ensemble complet de données peut être chargé en mémoire sous forme de table de hachage, consommant environ 300 Mo de mémoire. (Nous avons implémenté notre propre table de hachage. L'implémentation de Java prend une énorme surcharge de mémoire)
Chaque phrase peut alors être identifiée comme un tableau d'entiers.
Ceci est important, car le tri et les comparaisons sur les entiers sont beaucoup plus rapides que sur les chaînes.
Archiver les données
Le système conserve les données d'archive pour chaque jeton. Fondamentalement, ce sont des paires de
(Token, Frequency). Cependant, la table qui stocke les données serait si énorme que nous devions partitionner la table physiquement. Une fois que le schéma de partition est basé sur les ngrammes du jeton. Si le jeton est un seul mot, c'est 1 gramme. Si le jeton est une phrase de deux mots, il s'agit de 2 grammes. Et cela continue. Environ à 4 grammes, nous avons 1 milliard d'enregistrements, avec une table d'environ 60 Go.Traitement des flux entrants
Le système absorbe les phrases entrantes jusqu'à ce que la mémoire soit pleinement utilisée (oui, nous avons besoin d'un MemoryManager). Après avoir pris N phrases et enregistré en mémoire, le système s'arrête et commence à convertir chaque phrase en mots et en phrases. Chaque jeton (mot ou phrase) est compté.
Pour les jetons très fréquents, ils sont toujours conservés en mémoire. Pour les jetons moins fréquents, ils sont triés en fonction des ID (rappelez-vous que nous traduisons la chaîne en un tableau d'entiers) et sérialisés dans un fichier disque.
(Cependant, pour votre problème, puisque vous ne comptez que des mots, vous pouvez mettre tous les mappages de fréquences de mots en mémoire uniquement. Une structure de données soigneusement conçue ne consommerait que 300 Mo de mémoire pour 4 millions de mots différents. Un conseil: utilisez le caractère ASCII pour représentent des chaînes), ce qui est tout à fait acceptable.
En attendant, il y aura un autre processus qui sera activé une fois qu'il trouvera un fichier disque généré par le système, puis commencera à le fusionner. Puisque le fichier disque est trié, la fusion prendrait un processus similaire à celui du tri par fusion. Certaines conceptions doivent également être prises en compte ici, car nous voulons éviter trop de recherches aléatoires sur les disques. L'idée est d'éviter la lecture (processus de fusion) / écriture (sortie système) en même temps et de laisser le processus de fusion lire un disque tout en écrivant sur un autre disque. Cela revient à implémenter un verrouillage.
Fin de la journée
À la fin de la journée, le système aura de nombreux jetons fréquents avec une fréquence stockée en mémoire, et de nombreux autres jetons moins fréquents stockés dans plusieurs fichiers disque (et chaque fichier est trié).
Le système vide la carte en mémoire dans un fichier disque (trie-le). Maintenant, le problème devient la fusion d'un ensemble de fichiers de disque triés. En utilisant un processus similaire, nous obtiendrions un fichier disque trié à la fin.
Ensuite, la dernière tâche consiste à fusionner le fichier disque trié dans la base de données d'archives. Dépend de la taille de la base de données d'archive, l'algorithme fonctionne comme ci-dessous s'il est assez grand:
L'intuition est qu'après un certain temps, le nombre d'insertions deviendra de plus en plus petit. De plus en plus d'opérations se feront uniquement sur la mise à jour. Et cette mise à jour ne sera pas pénalisée par l'index.
J'espère que toute cette explication aiderait. :)
la source
Vous pouvez utiliser une table de hachage combinée à un arbre de recherche binaire . Implémentez un
<search term, count>dictionnaire qui vous indique combien de fois chaque terme de recherche a été recherché.Évidemment, itérer toute la table de hachage toutes les heures pour obtenir le top 10 est très mauvais. Mais c'est Google dont nous parlons, vous pouvez donc supposer que les dix premiers obtiendront tous, disons plus de 10 000 visites (c'est probablement un nombre beaucoup plus important cependant). Ainsi, chaque fois que le nombre d'un terme de recherche dépasse 10 000, insérez-le dans le BST. Ensuite, toutes les heures, vous n'avez qu'à obtenir les 10 premiers du BST, qui devraient contenir relativement peu d'entrées.
Cela résout le problème du top 10 de tous les temps.
La partie la plus délicate consiste à faire en sorte qu’un terme prenne la place d’un autre dans le rapport mensuel (par exemple, le «dépassement de pile» peut avoir 50 000 appels au cours des deux derniers mois, mais seulement 10 000 le mois dernier, tandis que «amazon» peut en avoir 40 000 pour les deux derniers mois mais 30 000 pour le mois dernier. Vous voulez que "amazon" vienne avant le "débordement de pile" dans votre rapport mensuel). Pour ce faire, je stockerais, pour tous les principaux termes de recherche (au-dessus de 10 000 recherches de tous les temps), une liste de 30 jours qui vous indique combien de fois ce terme a été recherché chaque jour. La liste fonctionnerait comme une file d'attente FIFO: vous supprimez le premier jour et en insérez un nouveau chaque jour (ou chaque heure, mais vous devrez peut-être stocker plus d'informations, ce qui signifie plus de mémoire / d'espace. Si la mémoire n'est pas un problème, faites it, sinon optez pour cette "approximation"
Cela semble être un bon début. Vous pouvez alors vous soucier d'élaguer les termes qui ont plus de 10 000 hits mais qui n'en ont pas eu beaucoup depuis longtemps et des trucs comme ça.
la source
cas i)
Conservez une table de hachage pour tous les termes de recherche, ainsi qu'une liste triée des dix premiers, distincte de la table de hachage. Chaque fois qu'une recherche se produit, incrémentez l'élément approprié dans la table de hachage et vérifiez si cet élément doit maintenant être remplacé par le 10ème élément de la liste des dix premiers.
O (1) recherche de la liste des dix premiers, et insertion max O (log (n)) dans la table de hachage (en supposant des collisions gérées par un arbre binaire auto-équilibré).
cas ii) Au lieu de maintenir une énorme table de hachage et une petite liste, nous maintenons une table de hachage et une liste triée de tous les éléments. Chaque fois qu'une recherche est effectuée, ce terme est incrémenté dans la table de hachage, et dans la liste triée, le terme peut être vérifié pour voir s'il doit basculer avec le terme après lui. Un arbre binaire auto-équilibré pourrait bien fonctionner pour cela, car nous devons également pouvoir l'interroger rapidement (plus d'informations à ce sujet plus tard).
De plus, nous maintenons également une liste des «heures» sous la forme d'une liste FIFO (file d'attente). Chaque élément «heure» contiendrait une liste de toutes les recherches effectuées au cours de cette heure particulière. Ainsi, par exemple, notre liste d'heures pourrait ressembler à ceci:
Ensuite, toutes les heures: si la liste a au moins 720 heures (c'est le nombre d'heures dans 30 jours), regardez le premier élément de la liste, et pour chaque terme de recherche, décrémentez cet élément dans la table de hachage du montant approprié . Ensuite, supprimez cet élément de la première heure de la liste.
Disons que nous sommes à l'heure 721 et que nous sommes prêts à regarder la première heure de notre liste (ci-dessus). Nous décrémentions les éléments gratuits de 56 dans la table de hachage, les images amusantes de 321, etc., puis supprimions complètement l'heure 0 de la liste car nous n'aurons plus jamais besoin de la regarder à nouveau.
La raison pour laquelle nous maintenons une liste triée de tous les termes qui permet des requêtes rapides est que toutes les heures après que nous parcourons les termes de recherche d'il y a 720 heures, nous devons nous assurer que la liste des dix premiers reste triée. Ainsi, lorsque nous décrémentons les `` éléments gratuits '' de 56 dans la table de hachage par exemple, nous vérifierions où ils appartiennent maintenant dans la liste. Parce que c'est un arbre binaire auto-équilibré, tout cela peut être accompli en un temps O (log (n)).
Edit: Sacrifier la précision pour l'espace ...
Il peut être utile d'implémenter également une grande liste dans le premier, comme dans le second. Ensuite, nous pourrions appliquer l'optimisation d'espace suivante dans les deux cas: Exécutez une tâche cron pour supprimer tous les éléments sauf les x premiers de la liste. Cela réduirait l'espace requis (et, par conséquent, rendrait les requêtes sur la liste plus rapides). Bien sûr, cela aboutirait à un résultat approximatif, mais cela est autorisé. x peut être calculé avant de déployer l'application en fonction de la mémoire disponible, et ajusté dynamiquement si davantage de mémoire devient disponible.
la source
Pensée approximative ...
Pour le top 10 de tous les temps
Pour le top 10 mensuel mis à jour toutes les heures:
Euh ... ça a du sens? Je n'ai pas pensé à ça comme je le ferais dans la vraie vie
Ah oui, j'ai oublié de mentionner, le "copier / aplatir" horaire requis pour les statistiques mensuelles peut en fait réutiliser le même code utilisé pour le top 10 de tous les temps, un bel effet secondaire.
la source
Solution exacte
Tout d'abord, une solution qui garantit des résultats corrects, mais qui nécessite beaucoup de mémoire (une grande carte).
Variante "de tous les temps"
Maintenez une carte de hachage avec des requêtes comme clés et leurs décomptes comme valeurs. De plus, gardez une liste des 10 requêtes les plus fréquentes à ce jour et le décompte du 10e dénombrement le plus fréquent (un seuil).
Mettez constamment à jour la carte lorsque le flux de requêtes est lu. Chaque fois qu'un nombre dépasse le seuil actuel, procédez comme suit: supprimez la 10e requête de la liste "Top 10", remplacez-la par la requête que vous venez de mettre à jour et mettez également à jour le seuil.
Variante "Mois dernier"
Gardez la même liste "Top 10" et mettez-la à jour de la même manière que ci-dessus. Aussi, gardez une carte similaire, mais cette fois, stockez des vecteurs de 30 * 24 = 720 comptage (un pour chaque heure) comme valeurs. Toutes les heures, procédez comme suit pour chaque clé: supprimez le compteur le plus ancien du vecteur, ajoutez-en un nouveau (initialisé à 0) à la fin. Supprimez la clé de la carte si le vecteur est entièrement nul. De plus, toutes les heures, vous devez calculer la liste des «10 meilleurs» à partir de zéro.
Remarque: Oui, cette fois, nous stockons 720 entiers au lieu d'un, mais il y a beaucoup moins de clés (la variante de tous les temps a une très longue queue).
Approximations
Ces approximations ne garantissent pas la solution correcte, mais consomment moins de mémoire.
la source
Top 10 des termes de recherche du mois dernier
L 'utilisation d' une indexation / structure de données efficace en mémoire, telle que des essais compacts (à partir d 'entrées wikipedia sur les essais ) définit approximativement une relation entre les besoins en mémoire et n - nombre de termes.
Dans le cas où la mémoire requise est disponible ( hypothèse 1 ), vous pouvez conserver des statistiques mensuelles exactes et les agréger chaque mois dans toutes les statistiques de temps.
Il y a aussi ici une hypothèse qui interprète le «mois dernier» comme une fenêtre fixe. Mais même si la fenêtre mensuelle glisse, la procédure ci-dessus montre le principe (le glissement peut être approché avec des fenêtres fixes de taille donnée).
Cela me rappelle la base de données à tour de rôle, à l'exception du fait que certaines statistiques sont calculées sur `` tous les temps '' (dans un sens où toutes les données ne sont pas conservées; rrd consolide les périodes sans tenir compte des détails en faisant la moyenne, en additionnant ou en choisissant des valeurs max / min, dans une tâche donnée, les détails perdus sont des informations sur les éléments à basse fréquence, qui peuvent introduire des erreurs).
Hypothèse 1
Si nous ne pouvons pas détenir des statistiques parfaites pour tout le mois, alors nous devrions être en mesure de trouver une certaine période P pour laquelle nous devrions être en mesure de tenir des statistiques parfaites. Par exemple, en supposant que nous ayons des statistiques parfaites sur une période P, qui va dans le mois n fois.
Les statistiques parfaites définissent la fonction
f(search_term) -> search_term_occurance.Si nous pouvons garder toutes
nles tables de statistiques parfaites en mémoire, les statistiques mensuelles glissantes peuvent être calculées comme ceci:ndes tableaux de statistiques parfaits)Cependant, si nous ne conservons que le top 10 au niveau agrégé (mensuel), nous pourrons supprimer beaucoup de données des statistiques complètes de la période fixe. Cela donne déjà une procédure de travail qui a des besoins de mémoire fixes (en supposant une limite supérieure sur une table statistique parfaite pour la période P).
Le problème avec la procédure ci-dessus est que si nous ne conservons les informations que sur les 10 principaux termes d'une fenêtre glissante (de la même manière pour tous les temps), les statistiques seront correctes pour les termes de recherche qui culminent dans une période, mais pourraient ne pas voir le statistiques pour les termes de recherche qui apparaissent constamment au fil du temps.
Cela peut être compensé en conservant des informations sur plus des 10 principaux termes, par exemple les 100 premiers termes, en espérant que les 10 premiers seront corrects.
Je pense qu'une analyse plus approfondie pourrait relier le nombre minimum d'occurrences requis pour qu'une entrée fasse partie des statistiques (ce qui est lié à l'erreur maximale).
(Pour décider quelles entrées devraient faire partie des statistiques, on pourrait également surveiller et suivre les tendances; par exemple, si une extrapolation linéaire des occurrences dans chaque période P pour chaque terme vous indique que le terme deviendra significatif dans un mois ou deux, vous peut déjà commencer à le suivre. Un principe similaire s'applique pour supprimer le terme de recherche du pool suivi.)
Le pire des cas pour ce qui précède est lorsque vous avez beaucoup de termes presque aussi fréquents et qu'ils changent tout le temps (par exemple, si le suivi de seulement 100 termes, alors si les 150 premiers termes sont également fréquents, mais les 50 premiers sont plus souvent au cours du premier mois et de peur que souvent, quelque temps plus tard, les statistiques ne soient pas conservées correctement).
Il pourrait également y avoir une autre approche qui n'est pas fixée dans la taille de la mémoire (enfin à proprement parler, ce qui précède ne l'est pas non plus), qui définirait une signification minimale en termes d'occurrences / période (jour, mois, année, tous les temps) pour laquelle conserver le Statistiques. Cela pourrait garantir une erreur maximale dans chacune des statistiques lors de l'agrégation (voir à nouveau le tournoi à la ronde).
la source
Qu'en est-il d'une adaptation de «l'algorithme de remplacement de page d'horloge» (également appelé «seconde chance»)? Je peux imaginer que cela fonctionne très bien si les demandes de recherche sont réparties uniformément (cela signifie que la plupart des termes recherchés apparaissent régulièrement plutôt que 5 millions de fois de suite et plus jamais).
Voici une représentation visuelle de l'algorithme: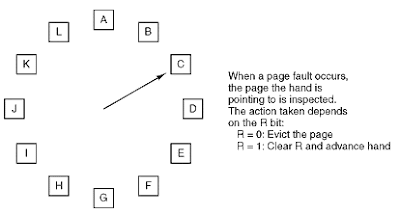
la source
Stockez le nombre de termes de recherche dans une table de hachage géante, où chaque nouvelle recherche entraîne l'incrémentation d'un élément particulier. Gardez une trace des 20 principaux termes de recherche; lorsque l'élément à la 11e place est incrémenté, vérifiez s'il a besoin d'échanger des positions avec # 10 * (il n'est pas nécessaire de garder le top 10 trié; tout ce qui vous importe est de faire la distinction entre le 10e et le 11e).
* Des vérifications similaires doivent être effectuées pour voir si un nouveau terme de recherche est à la 11ème place, donc cet algorithme se retrouve également dans d'autres termes de recherche - donc je simplifie un peu.
la source
parfois la meilleure réponse est "je ne sais pas".
Je vais prendre un coup plus profond. Mon premier instinct serait d'alimenter les résultats dans un Q. Un processus traiterait continuellement les éléments entrant dans le Q. Le processus maintiendrait une carte de
terme -> compter
chaque fois qu'un élément Q est traité, vous recherchez simplement le terme de recherche et incrémentez le nombre.
En même temps, je maintiendrais une liste de références aux 10 premières entrées de la carte.
Pour l'entrée qui a été actuellement implémentée, voyez si son nombre est supérieur au nombre du nombre de la plus petite entrée dans les 10 premiers (si ce n'est déjà dans la liste). Si c'est le cas, remplacez le plus petit par l'entrée.
Je pense que cela fonctionnerait. Aucune opération ne demande beaucoup de temps. Vous devrez trouver un moyen de gérer la taille de la carte de comptage. mais cela devrait suffire pour une réponse d'entrevue.
Ils n'attendent pas de solution, ils veulent voir si vous pouvez réfléchir. Vous n'avez pas à écrire la solution sur-le-champ ...
la source
queue,Qest une lettre :).Une façon est que pour chaque recherche, vous stockez ce terme de recherche et son horodatage. De cette façon, trouver les dix premiers pour n'importe quelle période de temps est simplement une question de comparaison de tous les termes de recherche dans la période donnée.
L'algorithme est simple, mais l'inconvénient serait une plus grande consommation de mémoire et de temps.
la source
Qu'en est-il de l'utilisation d'un arbre Splay avec 10 nœuds? Chaque fois que vous essayez d'accéder à une valeur (terme de recherche) qui n'est pas contenue dans l'arborescence, supprimez une feuille, insérez la valeur à la place et accédez-y.
L'idée derrière cela est la même que dans mon autre réponse . En supposant que les termes de recherche sont accédés uniformément / régulièrement, cette solution devrait très bien fonctionner.
Éditer
On pourrait aussi stocker d'autres termes de recherche dans l'arborescence (il en va de même pour la solution que je propose dans mon autre réponse) afin de ne pas supprimer un nœud auquel on pourrait accéder très prochainement. Plus on y stocke de valeurs, meilleurs sont les résultats.
la source
Je ne sais pas si je comprends bien ou non. Ma solution utilise le tas. En raison des 10 principaux éléments de recherche, je crée un tas de taille 10. Ensuite, mettez à jour ce tas avec une nouvelle recherche. Si la fréquence d'une nouvelle recherche est supérieure au haut du tas (Max Heap), mettez-la à jour. Abandonnez celui avec la plus petite fréquence.
Mais, comment calculer la fréquence de la recherche spécifique sera compté sur autre chose. Peut-être que comme tout le monde l'a dit, l'algorithme de flux de données ...
la source
Utilisez cm-sketch pour stocker le nombre de toutes les recherches depuis le début, gardez un tas min de taille 10 avec lui pour le top 10. Pour un résultat mensuel, gardez 30 cm-sketch / hash-table et min-heap avec, chacun commence comptage et mise à jour des derniers 30, 29 .., 1 jour. En tant que pass journalier, effacez le dernier et utilisez-le comme jour 1. Idem pour le résultat horaire, gardez 60 hash-table et min-heap et commencez à compter pour les 60, 59, ... dernières minutes. En une minute, effacez le dernier et utilisez-le comme minute 1.
Le résultat mensuel est précis dans une plage de 1 jour, le résultat horaire est précis dans une plage de 1 min
la source
Le problème n'est pas résolu universellement lorsque vous avez une quantité fixe de mémoire et un flux «infini» (pensez très très grand) de jetons.
Une explication approximative ...
Pour voir pourquoi, considérez un flux de jetons qui a un jeton particulier (c'est-à-dire un mot) T tous les N jetons dans le flux d'entrée.
Supposons également que la mémoire puisse contenir des références (identifiant et nombre de mots) à au plus M jetons.
Avec ces conditions, il est possible de construire un flux d'entrée où le jeton T ne sera jamais détecté si le N est suffisamment grand pour que le flux contienne des M jetons différents entre les T.
Ceci est indépendant des détails de l'algorithme top-N. Cela ne dépend que de la limite M.
Pour voir pourquoi cela est vrai, considérez le flux entrant composé de groupes de deux jetons identiques:
où les a et b sont tous des jetons valides différents de T.
Notez que dans ce flux, le T apparaît deux fois pour chaque ai et bi. Pourtant, il apparaît rarement assez rarement pour être vidé du système.
En commençant par une mémoire vide, le premier jeton (T) occupera un emplacement dans la mémoire (délimité par M). Ensuite, a1 consommera un emplacement, jusqu'à a- (M-1) lorsque le M est épuisé.
Quand aM arrive, l'algorithme doit abandonner un symbole alors que ce soit le T.Le symbole suivant sera b-1, ce qui provoquera le vidage de a-1, etc.
Ainsi, le T ne restera pas résidant en mémoire assez longtemps pour constituer un décompte réel. En bref, tout algorithme manquera un jeton de fréquence locale suffisamment basse mais de fréquence globale élevée (sur la longueur du flux).
la source