Existe-t-il des problèmes connus dans (et non dans ) qui ne sont pas terminés? Je crois comprendre qu'il n'y a actuellement aucun problème connu dans ce cas, mais cela n'a pas été exclu comme une possibilité.
S'il y a un problème qui est (et non ) mais pas , est-ce le résultat de l'absence d'isomorphisme existant entre les instances de ce problème et l'ensemble ? Dans ce cas, comment saurions-nous que le problème n'est pas plus difficile que ce que nous identifions actuellement comme l'ensemble ?
complexity-theory
np-complete
p-vs-np
vpiTriumph
la source
la source

Réponses:
Non, cela est inconnu (à l'exception des langages triviaux et , ces deux ne sont pas complets en raison de la définition de plusieurs réductions, généralement ces deux sont ignorés lors de l'examen de plusieurs réductions). L'existence d'un problème qui n'est pas complet pour rapport à plusieurs réductions de temps polynomiales impliquerait que qui n'est pas connu (bien que largement admis) . Si les deux classes sont différentes alors nous savons qu'il y a des problèmes dans qui ne sont pas complets pour cela, prenez n'importe quel problème dans .Σ ∗ N P N P P ≠ N P N P P


NP NP P NP
NP NP P
Si les deux classes de complexité sont différentes, alors selon le théorème de Ladner, il y a des problèmes qui sont intermédiaires, c'est-à-dire qu'ils sont entre et .P N P - c o m p l e t eNP P NP-complete
Ils sont toujours polynomiaux et réductibles aux problèmes , ils ne peuvent donc pas être plus difficiles que les problèmes .N P - c o m p l e t eNP-complete NP-complete
la source
Comme l'a déclaré @Kaveh, cette question n'est intéressante que si nous supposons ; le reste de ma réponse prend cela comme une hypothèse, et fournit principalement des liens pour vous donner encore plus faim. Dans cette hypothèse, par le théorème de Ladner, nous savons qu'il y a des problèmes qui ne sont ni en ni en ; ces problèmes sont appelés intermédiaire ou . Chose intéressante, le théorème de Ladner peut être généralisé à de nombreuses autres classes de complexité pour produire des problèmes intermédiaires similaires. De plus, le théorème implique également qu'il existe une hiérarchie infinie de problèmes intermédiaires qui ne sont pas poly-temps réductibles les uns aux autres dans .P N P C N P N P I N P I











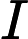


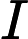
Malheureusement, même avec l'hypothèse il est très difficile de trouver des problèmes naturels qui seraient prouvablement (bien sûr, vous avez les problèmes artificiels provenant de la preuve du théorème de Ladner). Ainsi, même en supposant à ce moment, nous ne pouvons que croire que certains problèmes sont mais pas le prouver. Nous arrivons à de telles croyances lorsque nous avons des preuves raisonnables de croire qu'un problème n'est pas dans et / ou pas dans ; ou juste quand il a été étudié pendant longtemps et a évité de s'intégrer dans l'une ou l'autre classe. Il y a une liste assez complète de ces problèmes dans cette réponseN P I P ≠ N P N P I N P N P C P





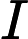






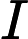






Fait intéressant, certains de ces problèmes (notables: factorisation et journal discret) ont des solutions temporelles polynomiales sur les ordinateurs quantiques (c'est-à-dire qu'ils sont en ). Certains autres problèmes (tels que l'isomorphisme des graphes) ne sont pas connus pour être dans , et des recherches sont en cours pour résoudre la question. D'un autre côté, on soupçonne que , donc les gens ne croient pas que nous aurons un algorithme quantique efficace pour SAT (bien que nous puissions obtenir une vitesse quadratique); c'est une question intéressante de s'inquiéter de quel type de problèmes de structure ont besoin pour être en .B Q P N P C ⊈













la source
Non NP Les problèmes sont connus pour être en P . S'il existe un algorithme à temps polynomial pour tout problème NP- complet, alors P = NP , car tout problème dans NP a une réduction du temps polynomial à chaque problème NP- complet. (C'est en fait ainsi que " NP- complet" est défini.) Et évidemment, si chaque problème NP- complet se situe en dehors de P , cela signifie que P ≠ NP . Nous ne savons pas vraiment pourquoi il est difficile de le montrer dans un sens ou dans l'autre; si nous connaissions la réponse à cette question, nous en saurions probablement beaucoup plus sur P etNP . Nous avons quelques techniques de preuve que nous savons ne pas fonctionner (relativisation et preuves naturelles, par exemple), mais nous n'avons pas d'explication de principe pour expliquer pourquoi ce problème est difficile.
S'il y a des problèmes dans NP qui ne sont pas dans P , alors il y a en fait une hiérarchie infinie de problèmes dans NP entre ceux dans P et ceux qui sont NP complets: c'est un résultat appelé théorème de Ladner .
J'espère que cela t'aides!
la source
Il y a des problèmes qui sont NP, mais personne ne sait qu'ils sont NP-Complete ou , comme l' isomorphisme de graphe 1 . Mais comme je sais qu'il n'y a pas de classe de complexité spéciale pour de tels problèmes, je me trompe peut-être.
Peut-être que c'est , par exemple avant l' algorithme AKS , personne ne sait que le test de primalité est ou NPC.

Il y a aussi certains problèmes qui sont NPC mais pas au sens fort ou faiblement NP-Complete , comme un problème à 2 partitions , signifie que si les nombres d'entrée sont dans l'ordre polynomial de la taille d'entrée, ces problèmes peuvent être résolus en (ou il y a un pseudo-algorithme temporel polynomial pour eux).
1 Problème similaire: l'isomorphisme du sous-graphe est NP-complet au sens fort.
la source